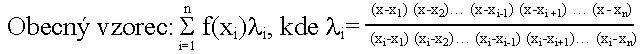
Lagrangeanův interpelační polynom

Lagrangeanův polynom je polynom nejmenšího stupně, který má v zadaných bodech předepsané hodnoty.

Jednou z možností, jak aproximovat nějakou funkci je najít polynom, který bude mít ve vybraných bodech stejné hodnoty, jako ona funkce. Pokud bude aproximovaná funkce rovněž polynom, a pokud zvolíme dostatečně mnoho bodů, získáme přímo aproximovanou funkci. Pokud tato funkce polynom nebude, pak získáme funkci "přibližně" podobou.

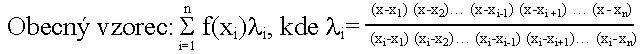
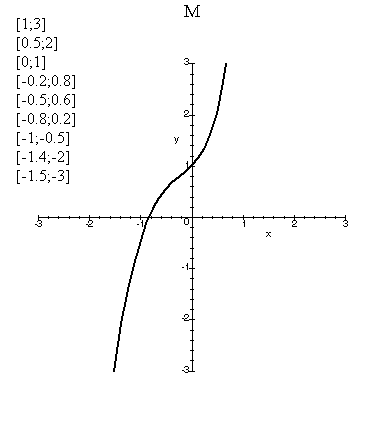
Pokusím se aproximovat zadanou funkci. Zvolil jsem 9 bodů, jejichž souřadnice jsou vypsány v grafu funkce. Výsledkem je polynom F(x) osmého stupně, který nabývá ve zvolených bodech stejných funkčních hodnot jako aproximovaná funkce.

F(x)=12.08654351*(x5-1.25x3+0.25x)*(x2+x+0.16)*(x+1.5)

-8.791208791*(x5-1.25x3+0.25x)*(x2+x+0.16)*(x+1.4)

-7.065979288*(x5-1.25x3+0.25x)*(x+0.2)*(x2+1.9x+2.1)

+19.75308642*(x3-x)*(x-0.5)*(x2+x+0.16)*(x2+1.9x+2.1)

-2.119793786*(x5-1.25*x3+0.25x)*(x+0.8)*(x2+1.9x+2.1)

-1.542317331*(x3-x)*(x2+x+0.16)*(x+0.5)*(x2+1.9x+2.1)

-10.41666666*(x2-x)*(x3-0.25)*(x2+x+0.16)*(x2+1.9x+2.1)

+0.1543209876*(x2+x)*(x2-0.25)*(x2+x+0.16)*(x2+1.9x+2.1)

+11.9047619*(x4-1.25x2+0.25)*(x2+x+0.16)*(x2+1.9x+2.1)

Graf získaného polynomu v intervalu –1,5;1,5 vypadá následovně:

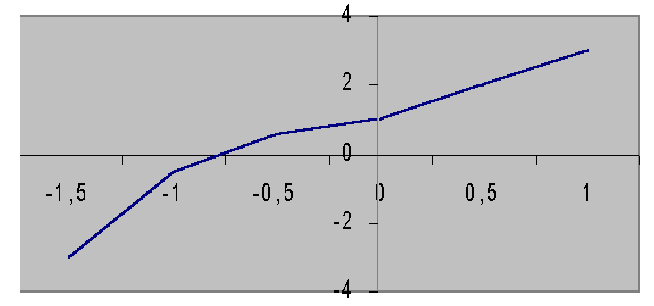Což je celkem uspokojivý výsledek. Zabrouzdáme-li však za hranice intervalu –1,5;1,5, zjistíme, že výsledek už zdaleka není tak uspokojivý, jak se zdál. Řešení, jak nalézt polynom, jehož graf se bude lépe podobat grafu zadané funkce, je buď zvolit více bodů nebo čtyři body, které budou věrněji popisovat průběh funkce. Získáme tak polynom třetího stupně, jehož grafem je kubická křivka, která by se mohla více podobat zadané funkci.